Explanation We can use here the formula for derivative of sin−1x, which is d dx sin−1x = 1 √1 − x2 As such to find derivative dy dx for y = sin−12x using chain rule is given by dy dx = 1 √1 − (2x)2 × d dx (2x) = 2 √1 −4x2 Answer link Explanation siny = x2 cosy( dy dx) = 2x dy dx = 2x cosy dy dx = 2x √1 − sin2y dy dx = 2x √1 − (x2)2 dy dx = 2x √1 −x4 Hopefully this helps!Simplify where possibley = sin−1(2x 1) This problem has been solved!
Untitled Document
1 quad 9.y=sin^(-1)((2x)/(1+x^(2)))
1 quad 9.y=sin^(-1)((2x)/(1+x^(2)))-Find Dy Dx If Y Sin 1 2x 1 X 2 hviezdoslavov kubín 7 ročník hugolin gavlovic valaska skola mravov stodola if f x x 3 x 2 x 1 then f 2 humanizmus a renesancia znaky ii rákóczi ferenc portrSolution Solution y = sin − 1 (1 x 2 2 x ) ⇒ sin y = 1 x 2 2 x ⇒ cos y = 1 − sin 2 y = 1 − (1 x 2 2 x ) 2 = 1 x 2 1 − x 2 Differentiating it wrt x, cos y d x d y = (1 x 2) 2 2 (1 x 2) − 2 x (2 x) ⇒ cos y d x d y = (1 x 2) 2 2 (1 − x 2) ⇒ d x d y = cos y 1 ((1 x 2) 2 2 (1 − x 2) ) ⇒ d x d y = 1 − x 2 1 x 2 ∗ ((1 x 2) 2 2 (1 − x 2) ) ⇒ d x d y = 1 x 2 2



Sin 1 X
Prove That Tan 1 1 2 Sin 1 2x 1 X2 Cos 1 1 Y2 1 Y2 X Y 1 Xy If Ixi 1 Y 0 And Xy 1 Math Inverse Trigonometric Functions Meritnation ComY Sin 1 2x 1 X 2 Find Dy Dx; find dy dx y sin 1 x2 1 x2 Mathematics TopperLearningcom 8s1l799 find dy dx y sin 1 x2 1 x2 Mathematics TopperLearningcom 8s1l799 Want to start a profitable Education Franchisee?
If y = (tan1 x) 2, prove that ( 1 x 2) 2 y 2 2x( 1Sin (θ), Tan (θ), and 1 are the heights to the line starting from the x axis, while Cos (θ), 1, and Cot (θ) are lengths along the x axis starting from the origin The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functionsIf \y = \sin^{ 1} \left( \frac{2x}{1 x^2} \right) \sec^{ 1} \left( \frac{1 x^2}{1 x^2} \right), 0 < x < 1,\ prove that \\frac{dy}{dx} = \frac{4}{1 x^2}\ ?
If `y=sin^(1)((x^21)/(x^21))sec^(1)((x^21)/(x^21))` then `dy/dx` is equal toIf y = sin (1x^2)/(1x^2), then dy/dx = Login Study Materials NCERT Solutions NCERT Solutions For Class 12 NCERT Solutions For Class 12 Physics;Y=3tan−1 x− √ x2 1 ⇒ y′ = 3 1 x− √ x2 1 2 1− x √ x2 1 ⇒ y′ = 3 1x 2−2x √ x2 1x 1 √ x2 1−x √ x2 1 ⇒ y′ = 3(√ x2 1−x



How To Differentiate Y Tan 1 2x 1 X 2 For The Inverse Trigonometric Function Quora




Example 3 Show I Sin 1 2x Root 1 X2 2 Sin 1 X Examples
If y = sin1 ( 2x / 1 x 2) sec1 ( 1 x 2 / 1 x 2) , show that dy/dx = 4 / ( 1 x 2) Share with your friends Share 3 Let y = sin1 2 x 1 x 2 sec1 1 x 2 1x 2 = sin1 2 x 1 x 2 cos1 1x 2 1 x 2 LetY 4 1 3 X 2 Graph;X 2y 5 Y 2x 2 Graphically;



3



10 Derivative Find Dy By Dx Of Y Sin 1 2x Upon 1 X2 Youtube
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreAd by Grammarly Fast Simple Free Get rid of typos, grammatical mistakes, and misused words with a single click Try now Learn More 3 Answers Ruchi Chhabra, Post Graduation Mathematics, Lady Shri Ram College for Women (1986)Wzór Na Zamianę Km H Na M S;



49 60 Find The Derivative Of The Function Simplify Chegg Com



Answered G X U G Fx 00 O 7 26 Find F X Bartleby
Best answer Let y = sin1( (2x 1)/ (1 4x)) = sin1( (2x x 2)/ (1 (2x)2)) Let 2x = tanθ ⇒ θ = tan12x then we have y = sin1(2tanθ/ (1 tan2θ)) = sin1(sin2θ) = 2θ = 2tan12x Differentiating both sides wrt x, we get Please log in or register to add a comment ← Prev Question Next Question → If y= sin^(1)((2x)/(1x^2)) sec^(1)((1x^2)/(1x^2)) , prove that (dy)/(dx)=4/(1x^2)Find dy/dx of ,y=1/sin(2x/1x^2) Ask questions, doubts, problems and we will help you menu myCBSEguide Courses CBSE Entrance Exam Competitive Exams ICSE & ISC Teacher Exams UP Board Uttarakhand Board Features Online Test Practice Homework Help Downloads CBSE Videos



Assignment 1 Exploring Sine Curves



Links Forward Inverse Trigonometric Functions
Derivative of 1/sqrt(1x^2) by x = x/(sqrt(1x)*sqrt(x1)*(x^21)) Show a step by step solution;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolution Given y = sin 1 (2x/ (1 x 2) sec 1 (1 x 2 )/ (1 – x 2) Put x = tan θ θ = tan 1 x So y = sin 1 2 tan θ / (1 tan 2 θ) cos 1 (1 – tan 2 θ)/ (1 tan 2 θ) = sin 1 sin 2θ cos 1 cos 2θ




Tan11 Example 7 Show That I Sin 1 2x V Sin 1 2x 11 X2 2



How To Find Derivative Of Y Sin 2x 1 X 2 Quora
Get an answer for 'Find the exact length of the curve y= (xx^2)^1/2 sin^1(x)^1/2 I get confused after I try to square y' I would appreciate if all steps are clearly shown' and find homeworkDifferentiate with respect to x Panchapakesan6616 is waiting for your help Add your answer and earn pointsY = sin − 1 (1 x 2 2 x ) Differentiating above equation wrt x , we have d x d y = 1 − ( 1 x 2 2 x ) 2 1 ( ( 1 x 2 ) 2 2 ( 1 x 2 ) − 2 x ( 2 x ) )



Simplify Tan 1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X 1 Y 0 And Xy 1 Sarthaks Econnect Largest Online Education Community
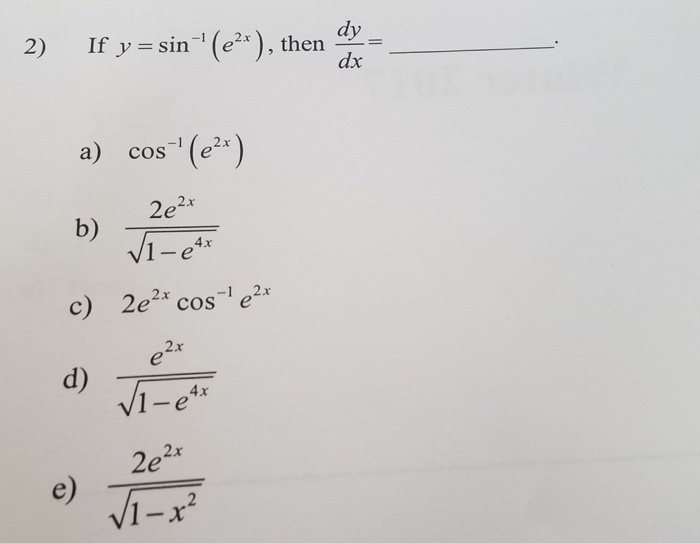



If Y Sin 1 E 2x Then Dy Dx A Chegg Com
Ex 53, 9 Find 𝑑𝑦/𝑑𝑥 in, y = sin^(−1) (2𝑥/( 1 2𝑥2 )) 𝑦 = sin^(−1) (2𝑥/( 1 2𝑥2 )) Putting x = tan θ 𝑦 = sin^(−1) (2𝑥/( 1COMEDK 08 If y = sin1 ((5x12 √1 x2/13)) , then (dy/dx) = (A) (3/√1 x2) (B) (12/√1 x2) (1/√1 x2) (D) (1/√1 x2) Check A NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 53 Find in the following Ex 53 Class 12 Maths Question 1 2x 3y = sinx Solution 2x 3y = sinx Differentiating wrt x, => Ex 53 Class 12 Maths Question 2




Find Dy Dx Of Y Sin 1 2x 1 X 2 Youtube




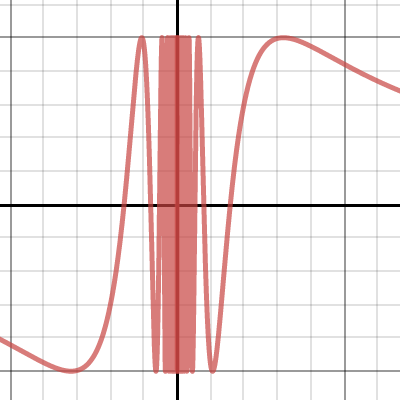
Which Graph Represents The Function Y 2 Sin 1 2 X Look At The Graphs Below For The Answer Brainly Com
Y X 2 2x 2 GraphDraw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs Since y = sin 1 x is the inverse of the function y = sin x, the function y = sin1 x if and only if sin y = xBut, since y = sin x is not onetoone, its domain must be restricted in order that y = sin1 x is a function To get the graph of y = sin1 x, start with a graph of y = sin x Restrict the domain of the function to a onetoone region typically is used (highlighted in red at




How Do You Differentiate F X 1 Sin 2x 1 Sin 2x Socratic



If Y 2 Tan 1 X Sin 1 2x 1 X 2 For All X Then Y Sarthaks Econnect Largest Online Education Community
Y X 2 2x 1 Graph;The sum of inverse sines of both values is equal to 60 ∘ and it is expressed in mathematical form sin − 1 x sin − 1 2 x = π 3 The inverse trigonometric equation can be solved by applying the sum rule of inverse sine functions to obtain the value of x but it makes the simplification more complicated in this case 01 if y = (1 sin2x/1 sin 2x) 1/2 show that dy/dx sec 2 (π/4 – x) = 0 donot go shortcut if y = log tan (∏/4 x/2) show that dy/dx = sec x donot go shortcut if y = log (x (1 x 2) 1/2 ) prove that dy/dx = 1/log (x (1 x 2) 1/2) 1/ (1 x 2) 1/2 Find dy/dx y = x x e (2x 5) mention each and every step



Find Dy Dx Y Sin 1 2x 1 X 2 1 2 X 1 2 Sarthaks Econnect Largest Online Education Community




Find Dy Dx In The Following Y Sin 1 2x 1 X 2
Y Cos X Pi 3 2;Y X 2 Graph And Table;Y Sin 1 2x 1 X 2 Find Dy Dx čítanie pre prvákov online šalát z červenej kapusty s jablkom čo sa oplatí študova




Sin 1 X




Find The Value Of Cot1 2 Cos 1 2x 1 X2 Sin 1 1 Y2 1 Y2 Maths Inverse Trigonometric Functions Meritnation Com
Calculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculoIf y=f (2x1/x^21) and f'x=sinx^2, Can you find dy/dx?Y X 2 Z 2 Graph;
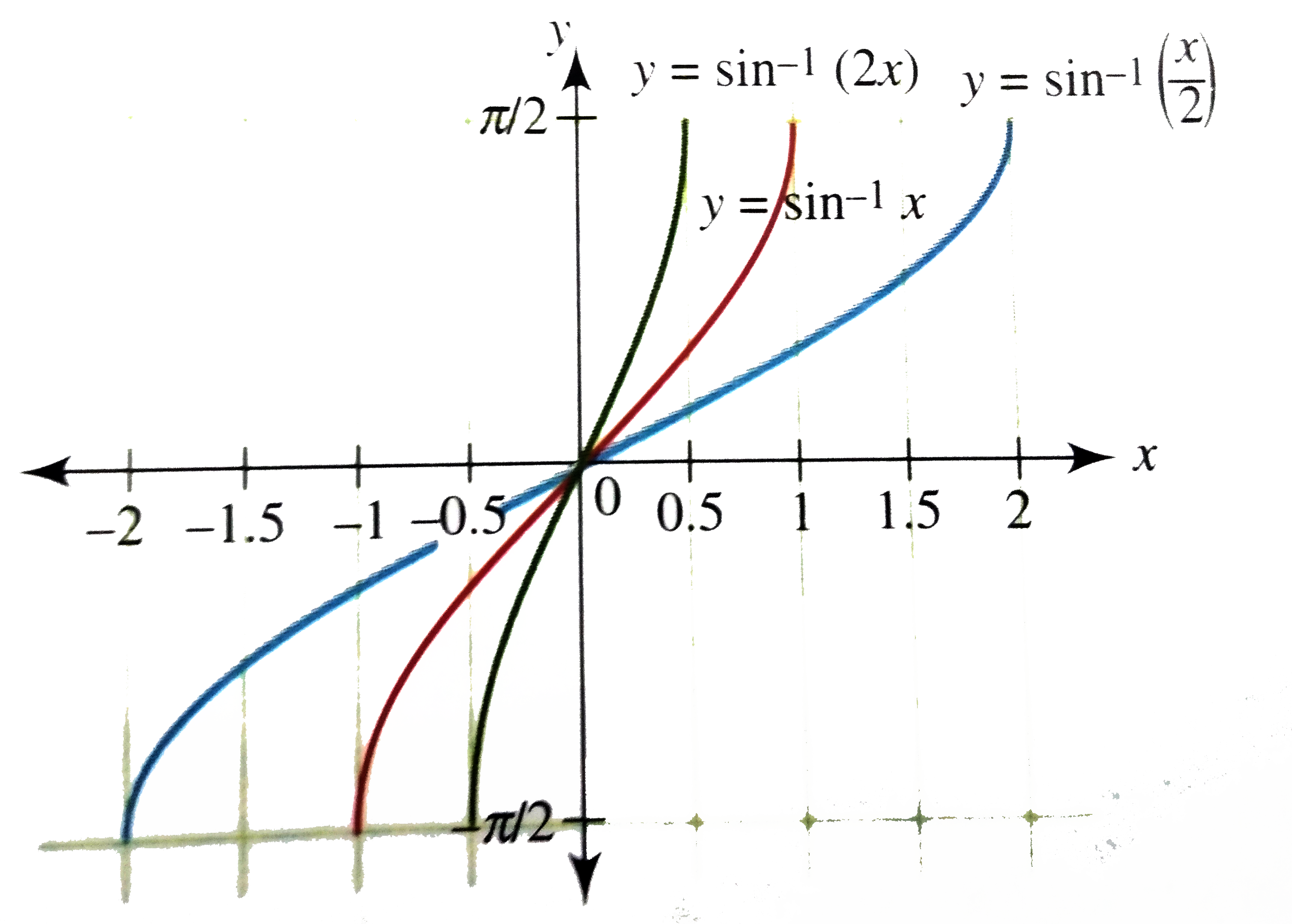



Draw The Graph Of Y Sin 1 2x 1 X 2



Graph Of Y Sin 1 2 X In Urdu Hindi Youtube
Find dy/dx for y=sin^1(1x^2/1x^2) 1118 gshinde gshinde Math Secondary School answered Find dy/dx for y=sin^1(1x^2/1x^2) 1 See answer gshinde is waiting for your help Add your answer and earn points rishu6845 rishu6845 Answer plzz give me brainliest ans and plzzzz follow meX 2 Y 4 5 X Y 2 7 10;Y X 3 Graph Name;




If Y Sin 1 2x1 X 2 Sec 1 1 X 21 X 2 Show That Dydx 4 1 X 2



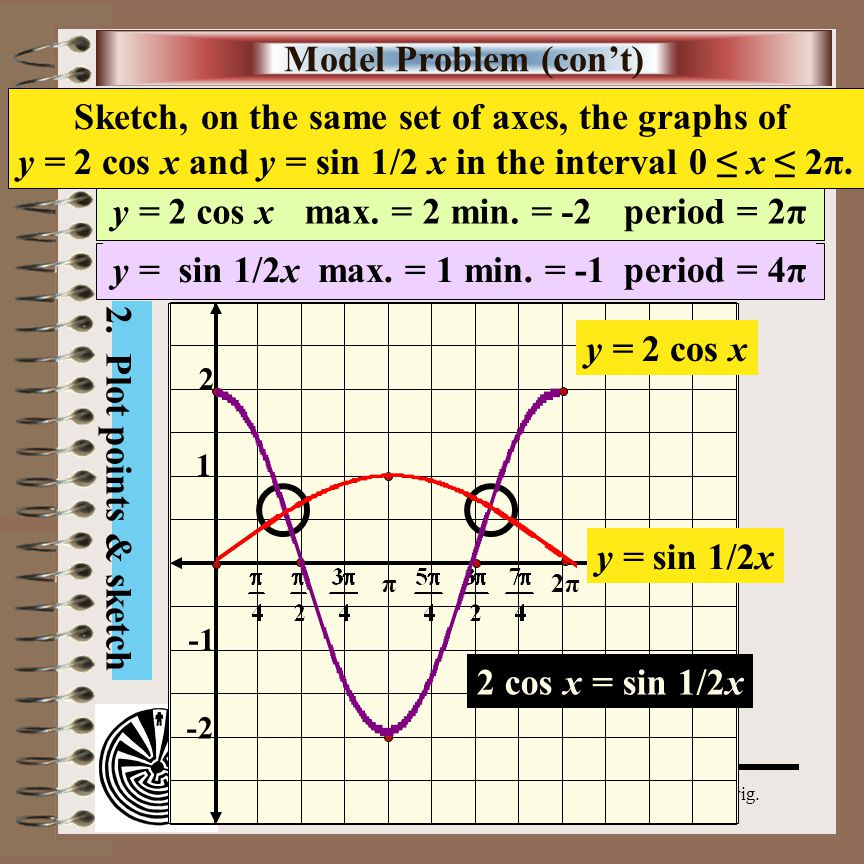
Solution 1 A On The Same Set Of Axes Sketch And Label Graphs Of Y Sin 1 2 X And Y 2 Cos X As X Varies From 0 To 2 Pi Radians B Using
X 2 Y 2 Z 2 Formula; Get an answer for '`y = x sin^1(x) sqrt(1 x^2)` Find the derivative of the function Simplify where possible' and find homework help for other Math questions at eNotes Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange



Untitled Document




Se13e01 01 Gif
See the answer See the answer See the answer done loading Find the derivative of the function Simplify where possible y = sin−1(2x 1) Best Answer This is the best answerY X 2 2x 5; 1 The "identity" arcsin( 2x 1 x2) = 2arctanx does not hold for all x You can see this by comparing the ranges of the two sides The arcsine function has − π / 2, π / 2 as its range, but twice the arctangent function has ( − π, π) as its range In particular, if x > 1, then 2arctanx > π / 2, and likewise if x < − 1 then



Draw The Graph Of Y Sin 1 2x 1 X 2
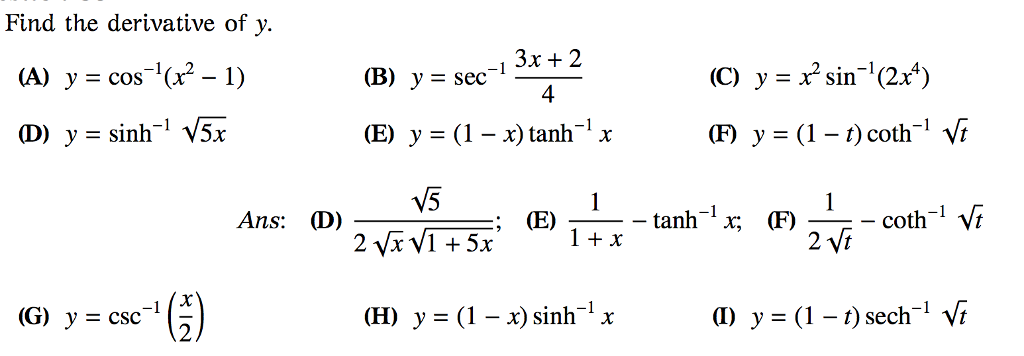



Find The Derivative Of Y A Y Cos 1 X 2 1 Chegg Com
Consider the triangle T ⊂ S with vertices (0,0), (1/2,1/2), (1/2,1) Thus, T is defined by the inequalities 0 < x < y < 2x < 1 For every (x,y) in T, xy > x2 and x2 y2 < 5x2 Show that all solutions of y'= \frac {xy1} {x^21} are of the form y=xC\sqrt {1x^2} without solving the ODE Show that all solutions of y′ = x21xy1 sin1 ( x root (1x) root(x)root(1x^2) ) pls answer , I have a test tomorrow / Share with your friends Share 11 take x = sin a & rootx = sin b then it will be sin^1 (sin a root (1 sin^2b) sin b root (1sin^2a) ) sin^1 (sina cosb sinb cos a) sin^1 (sin (ab)) a b sin^1x sin^1rootx 18 ;Let y = sin1 ((2x/1x2)), 0 < x < 1 and 0 < y < (π/2), then (dy/dx) is equal to Q Let $y = \sin^{1} \left(\frac{2x}{1x^{2}}\right), 0 x 1$ and $ 0 y \frac{\pi}{2}, $ then $\frac{dy}{dx} $ is equal to




If Y Sin 1 X 1 X2 1 2 Show That 1 X2 D2y Dx2 3x Dy Dx Y 0 Explain In Great Detail Mathematics Topperlearning Com Wa3tv55
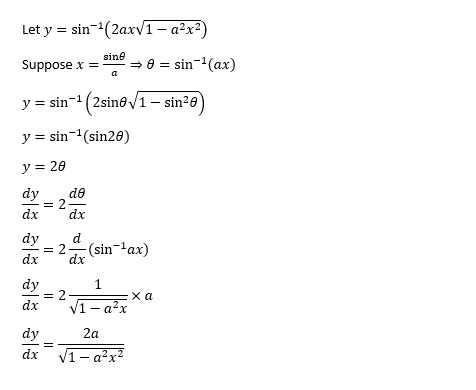



D Dx Sin 1 2ax 1 A 2x 2
If y=sin^(1)((2x)/(1x^2))sec^(1)((1x^2)/(1x^2)),\ \ 0Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyWww Statpedu Sk Inovované Učebné Osnovy;



Graph Sine And Cosine Functions



What Is The Value Of Tan1 2 Sin 1 2x 1 X X Cos 1 1 Y Y 1 Y Y Quora
Graph y=sin(1/2x) Use the form to find the variables used to find the amplitude, period, phase shift, and vertical shift Find the amplitude Amplitude Find the period of Tap for more steps The period of the function can be calculated using Replace with in the formula for periodIf y = sin^1 (2x √ (1 x^2)), 1√ (2)≤ x ≤ 1√ (2) , then dydx is equal toDear Teachers, Students and Parents, We are presenting here a New Concept of Education, Easy way of selfStudy This is an AudioVisual e Guide,




Show That The Function F X X Sin 1 X When X 0 0 When X 0 Is Continuous Butnot Diff Youtube




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6
X 2 Y 2 Z 2 16;2x (1x 2)(2x)/(1x 2) 2 = cos (1x 2)/(1x 2) 2x 2x 3 2x2x 3/(1x 2) 2 = cos (1x 2)/(1x 2) 4x/(1x 2) 2 = (4x/(1x 2) 2 ) cos ((1x 2)/(1x 2)) Hence option (3) is the answer Was Ex 53, 14 Find 𝑑𝑦/𝑑𝑥 in, y = sin–1 (2𝑥 √ (1−𝑥^2 )) , − 1/√2 < x < 1/√2 y = sin–1 (2𝑥 √ (1−𝑥^2 )) Putting 𝑥 =𝑠𝑖𝑛𝜃 𝑦 = sin–1 (2 sin𝜃 √ (1−〖𝑠𝑖𝑛〗^2 𝜃)) 𝑦 = sin–1 ( 2 sin θ √ (〖𝑐𝑜𝑠〗^2 𝜃)) 𝑦 ="sin–1 " (〖"2 sin θ" 〗cos𝜃 ) 𝑦 = sin–1 (sin〖2 𝜃)〗 𝑦 = 2θ Putting value of θ = sin−1 x 𝑦 = 2 〖𝑠𝑖𝑛〗^ (−1) 𝑥 Since x = sin θ ∴




Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5
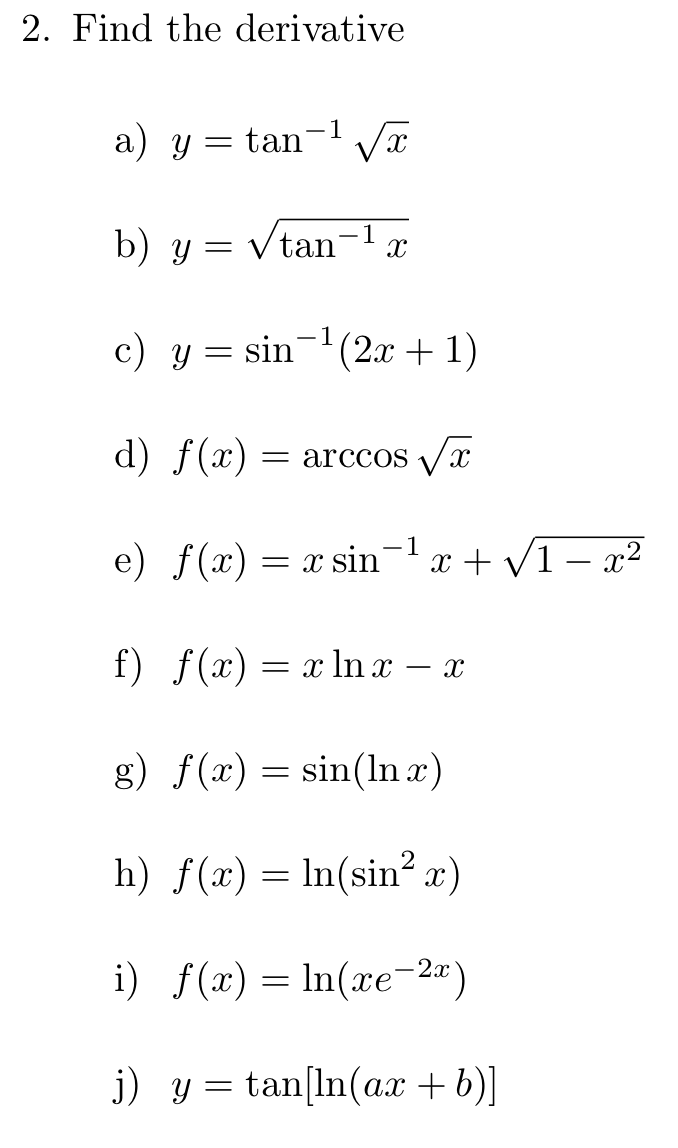



2 Find The Derivative A Y Tan 1 Vx B Y Vtan 1 A Chegg Com
Prove that sin1 x sin1 y = sin1 (x √1y 2 y √1x 2) if x 2 y 2 ≤ 1Graph y=1/2*sin (x) y = 1 2 ⋅ sin(x) y = 1 2 ⋅ sin ( x) Use the form asin(bx−c) d a sin ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 1 2 a = 1 2 b = 1 b = 1 c = 0 c = 0 d = 0 d = 0 Find the amplitude a a Amplitude 1 2 1 2X 2 Y 1 2x 3y K;



Assignment 1 Exploring Sine Curves




Differentiate Tan 1 2x 1 X 2 With Respect To Sin 1x 2x 1 X 2 Brainly In
So,the 'y' in the question,arcsin(2x/1x^2) is a little difficult to handle,so a smart substitution has been done in the form of x=tan θ which simplifies the 'y' to be equal to 2 arctan(x) Now,y=2tan^1(x) Differentiating both sides,we get dy/dx=2*1/1x^2 as derivative of tan^1(x) is 1/1x^2 And dy/dx is what was asked in the question Cheers )




Exercise 4 1 Sine Function And Inverse Sine Function Problem Questions With Answer Solution



If Y F 2x 1 X 2 1 And F X Sinx 2 Can You Find Dy Dx Quora




Find Dy Dx Y Sin 1 X2 1 X2 Mathematics Topperlearning Com 8s1l799




Differentiate With Respect To X Y Sin 1 2x 1 X2 Brainly In
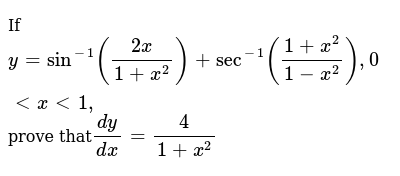



If Y Sin 1 2x 1 X 2 Sec 1 1 X 2 1 X 2 0ltxlt1




1 Find The Derivative Of The Following Functions A Chegg Com



Pinkmonkey Com Trigonometry Study Guide Supplementary Problems




Find Dy Dx For Y Sin 1 2xsqrt 1 X 2 1 Sqrt2 X 1 Sqrt2 Mathematics Shaalaa Com
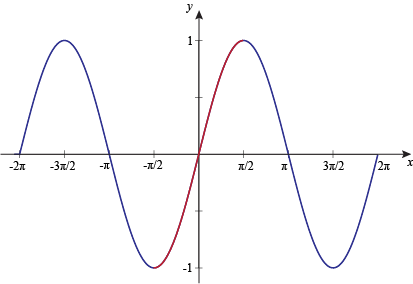



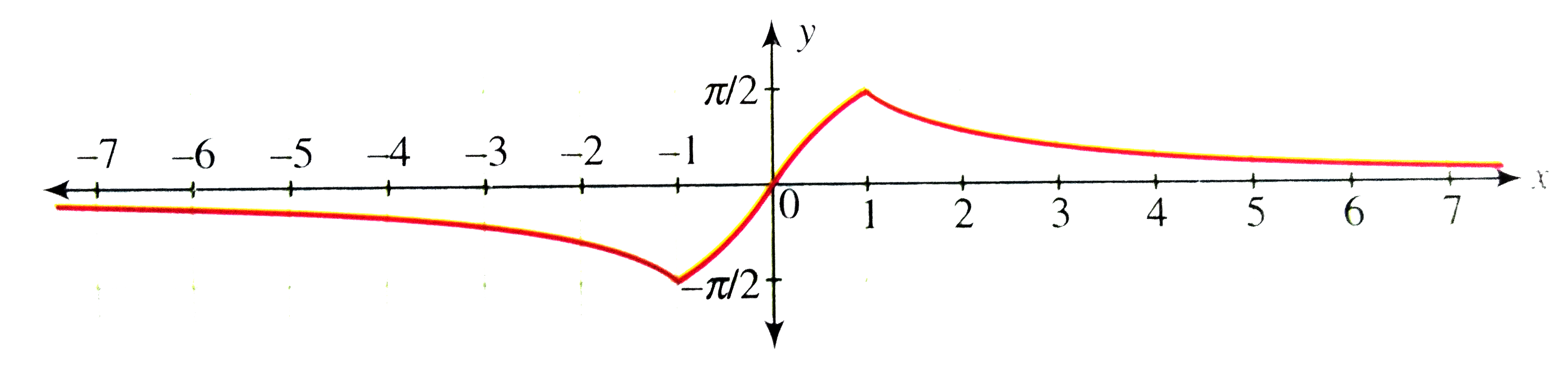
Graph Of Inverse Sine Function




If Y Sin 1 2x 1 X 2 Sec 1 1 X 2 1 X 2 0 X 1




Ex 5 3 14 Find Dy Dx In Y Sin 1 2x Root 1 X2 Cbse



1




Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5




If Y Sin 1 2x 1 X 2 Then Dy Dx Is Equal T




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6



Pinkmonkey Com Trigonometry Study Guide 5 4 Graphs Of Trigonometric Functions




Find The Derivative Of The Function Y 6 Sin 1 Chegg Com




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6



How To Differentiate Y Tan 1 2x 1 X 2 For The Inverse Trigonometric Function Quora




If Y Sin 2 Cot 1 Sqrt 1 X 1 X Then Dy Dx Is Youtube




Ex 5 3 12 Find Dy Dx In Y Sin 1 1 X2 1 X2 Chapter 5




Y Sin 1 2x 1 X 2 Find Dy Dxif Dy Dx 2cos 1xthis Is Class 12 The Problem Plz Help Brainly In




Find Dy Dx In The Following Y Sin 1 2xsqrt 1 X 2 1
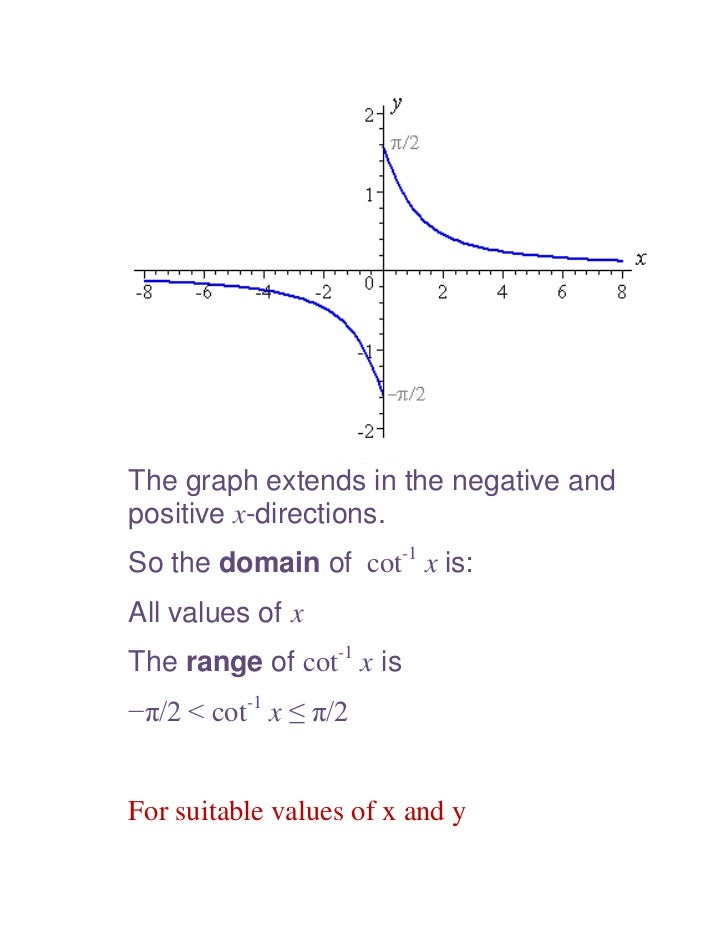



Inverse Trigonometric Functions Xii 1



3



Writeup1 Html
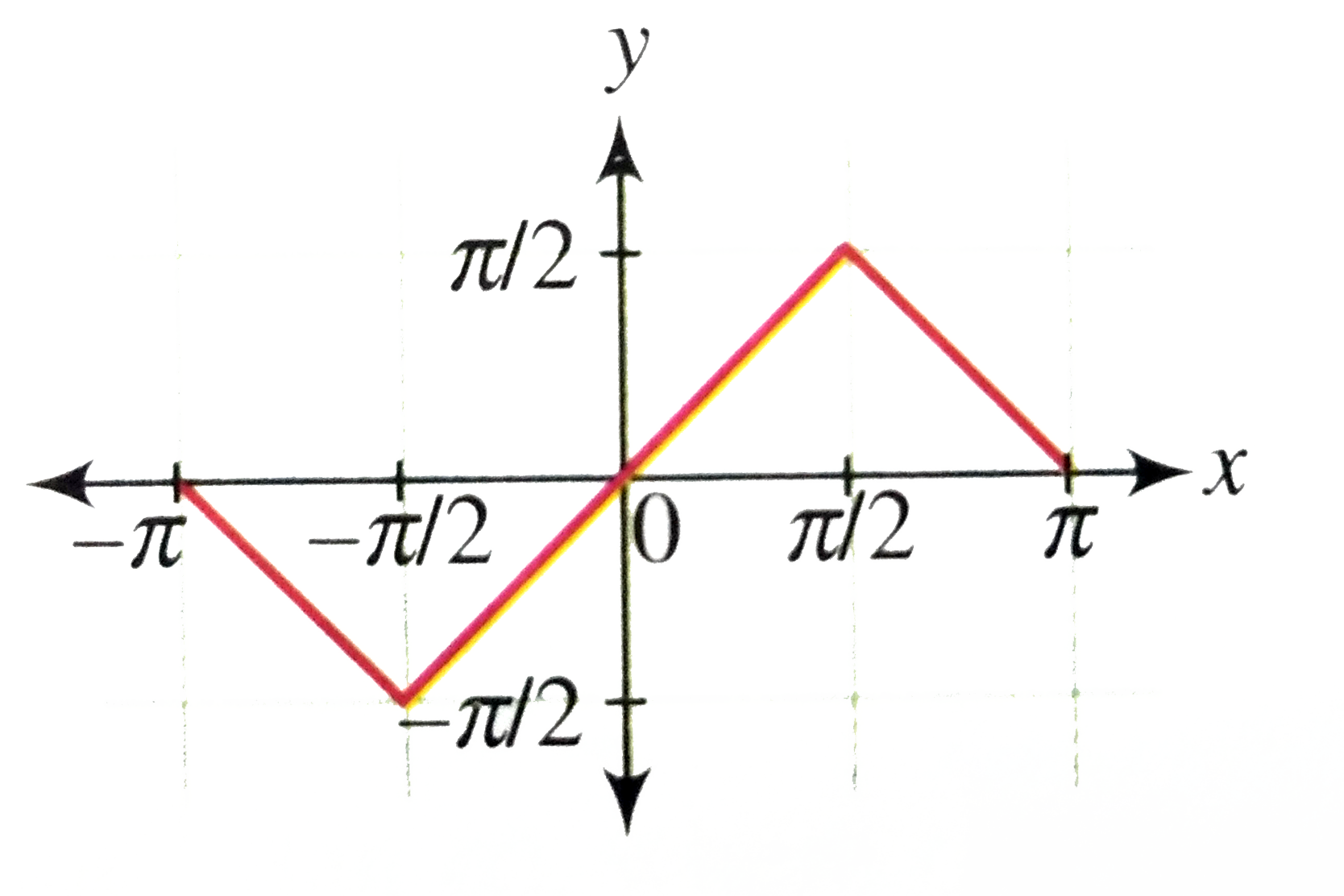



Draw The Graph Of Y Sin 1 2x 1 X 2
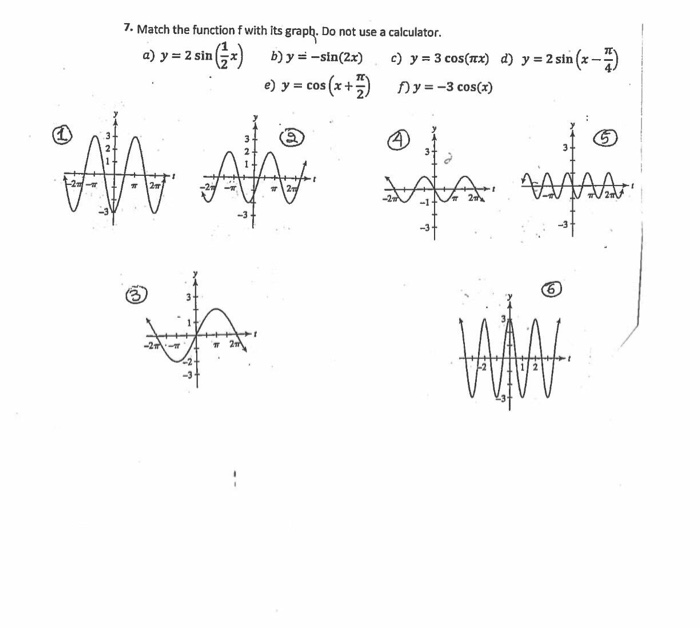



Match The Function F With Its Graph Do Not Use A Chegg Com



Assignment 1 Exploring Sine Curves




Solve For X 3sin 1 2x 1 X2 4cos 1 1 X2 1 X2 2tan 1 2x 1 X2 Pie 3 Brainly In
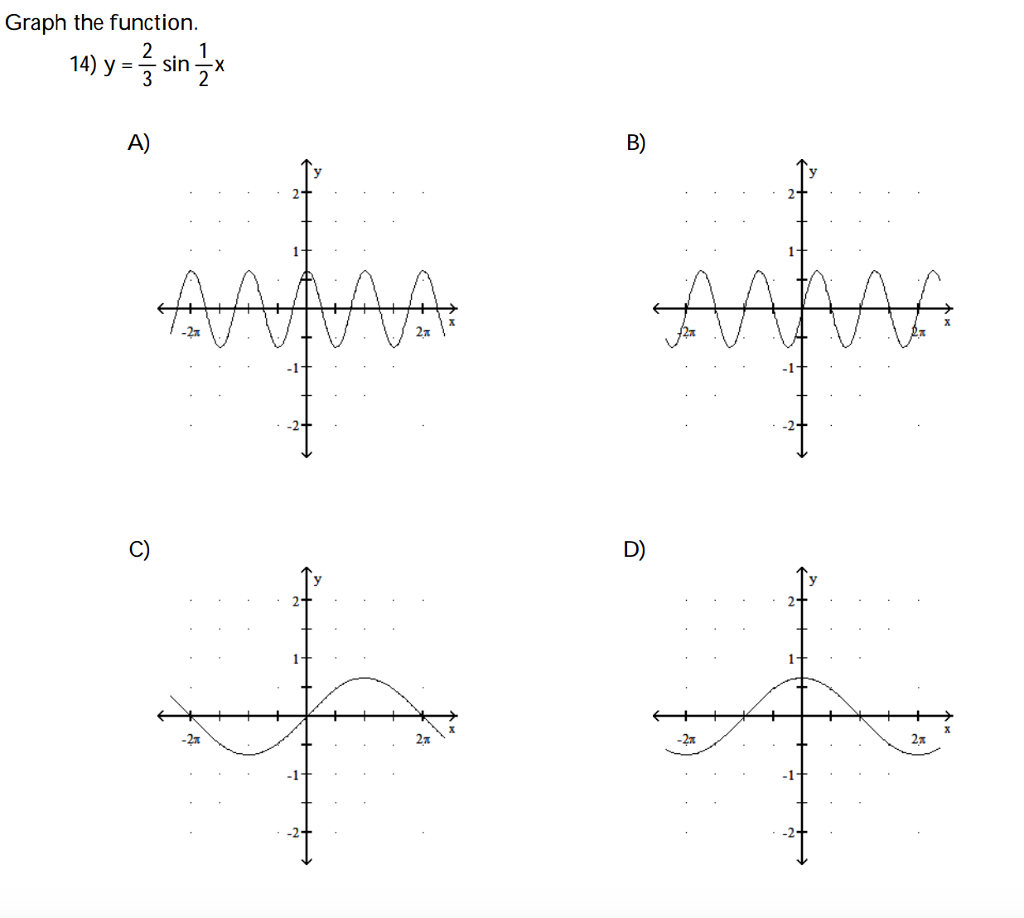



Graph The Function Y 2 3 Sin 1 2 X Chegg Com



Differentiate The Following With Respect To X Sin 1 2 X 1 3 X 1 36 X Sarthaks Econnect Largest Online Education Community



Sin 1 X And X Sin 1 X Limit Examples



Assignment 1 Write Up



Solved Derivative Of Trigonometric And Inverse Trigonometric Functions Find Dy Dx 1 Y Sin X2 3x 1 2 Y Cos 2 2x 1 3 Y Tan Vx2 Course Hero



If Y 2 Tan 1 X Sin 1 2x 1 X 2 For All X Then Y Sarthaks Econnect Largest Online Education Community



Solved Derivative Of Trigonometric And Inverse Trigonometric Functions Find Dy Dx 1 Y Sin X2 3x 1 2 Y Cos 2 2x 1 3 Y Tan Vx2 Course Hero




Prove That 2 Tan Inverse 1 X Sin Inverse 2x X2 1 Brainly In




Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2
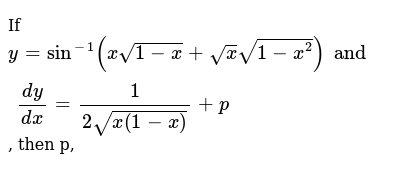



If Y Sin 1 X Sqrt 1 X Sqrtx Sqrt 1 X 2 And Dy



Aim What S The A In Y A Sin X All About Ppt Video Online Download




The Derivative Of Tan 1 2x 1 X 2 With Respect To Sin 1 2x 1 X 2 Is Youtube




Find Dy Dx In The Following Y Sin 1 2x 1 X 2 Youtube



Sin




Find Dy Dx For Y Sin 1 2x 1 X 2 Mathematics Shaalaa Com




Multivariate Example 2 Constrained Expression Evaluated Using G X Y Download Scientific Diagram




Find The Derivative Of The Function Y Sin 1 2x Chegg Com
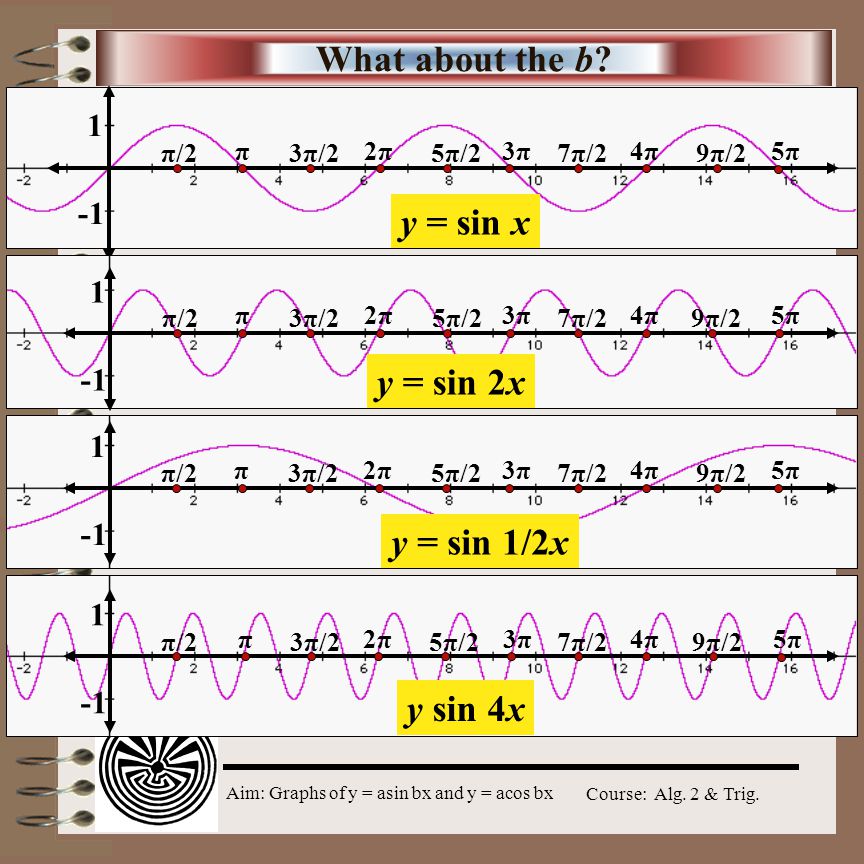



Aim What S The A In Y A Sin X All About Ppt Video Online Download



If Y Sin 12x 1 X 2 Then Which Of The Following Is Not Correct Sarthaks Econnect Largest Online Education Community




Prove That Tan 1 1 2 Sin 1 2x 1 X2 Cos 1 1 Y2 1 Y2 X Y 1 Xy If Ixi 1 Y 0 And Xy 1 Maths Inverse Trigonometric Functions Meritnation Com




Differentiation Of Cos Inverse 2x By 1 X Square
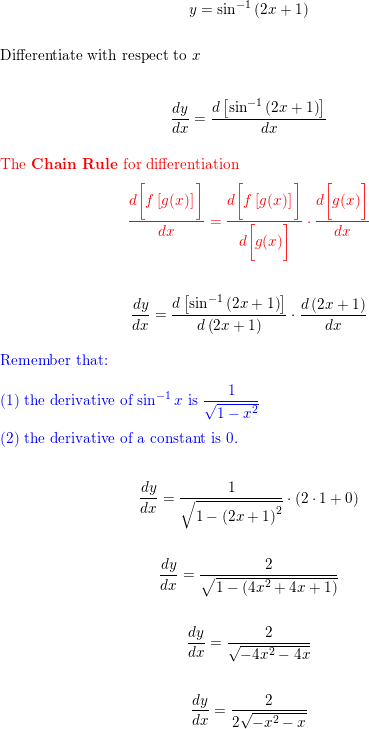



Find The Derivative Of The Function Simplify Where Possible Quizlet




D Y D X Y 2 X Zonealarm Results




If Y Sin 1 2x 1 X 2 Sec 1 1 X 2 1 X 2 0ltxlt1




Differentiate W R T X Sin 1 2 X 1 1 4 X




Solved Find The First Derivative Of The Following Functio Chegg Com



Graph Sine And Cosine Functions



If Y 2 Tan 1 X Sin 1 2x 1 X 2 For All X Then Y Sarthaks Econnect Largest Online Education Community



How To Find Dy Dx Of Sin 1 2x And Y Sin 1 2x 3 Quora



Find The Value Of Tan1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X 1 Y 0 And Xy 1 Sarthaks Econnect Largest Online Education Community




If Y Sin 1 2x 1 X 2 Then Find Dy Dx Youtube




Y Sin 2sin 1x Prove That 1 X 2 Y2 Xy1 4y Maths Continuity And Differentiability Meritnation Com



What Is The Nth Derivative Of Sin Inverse 2x 1 X 2 Quora




If Y Sin 1 2x 1 X 2 1 2 X 1 2 Then Dydx Is Equal To



Pinkmonkey Com Trigonometry Study Guide Supplementary Problems




Differentiate Sin Tan 1 2x W R T X And Express The Result Free From Trigonometric Symbols Own Classes



0 件のコメント:
コメントを投稿